M1MisakaMikoto
M1MisakaMikoto
Articles11
Tags0
Categories2
回到首页
文章归档
我的朋友
给我赞助
关于博主

Categories

Archive

Recent Posts

© 2023 M1MisakaMikoto Powered by Hexo & Nexmoe








Dijkstra算法求最短路径

Dijkstra算法求最短路径

2023年11月01日 CS

迪杰斯特拉(Dijkstra)

引子[摘自:最短路径算法-迪杰斯特拉(Dijkstra)算法 - 知乎 (zhihu.com)]

最短路径算法-迪杰斯特拉(Dijkstra)算法

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先遍历思想)，直到扩展到终点为止。

基本思想

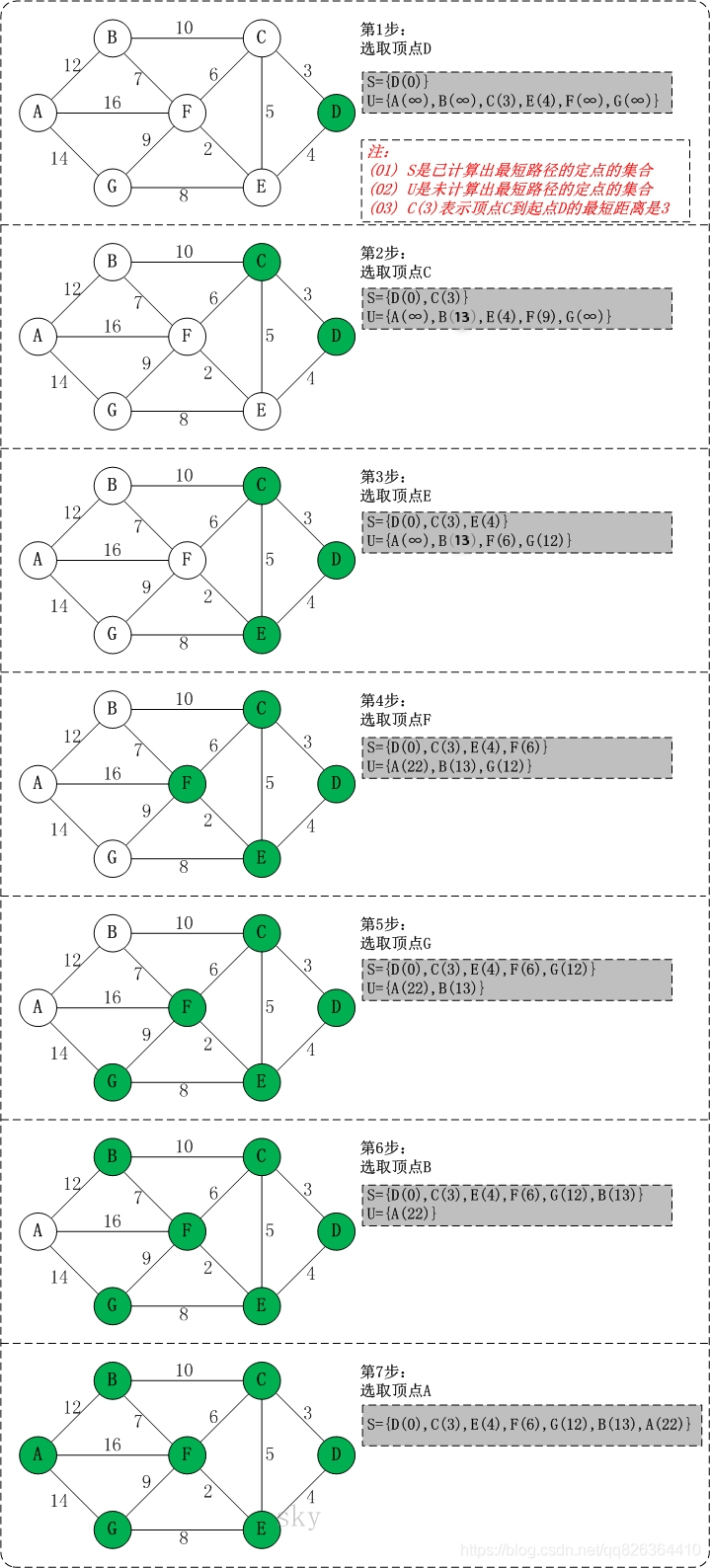
  1. 通过Dijkstra计算图G中的最短路径时，需要指定一个起点D(即从顶点D开始计算)。
  2. 此外，引进两个数组S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点D的距离)。
  3. 初始时，数组S中只有起点D；数组U中是除起点D之外的顶点，并且数组U中记录各顶点到起点D的距离。如果顶点与起点D不相邻，距离为无穷大。
  4. 然后，从数组U中找出路径最短的顶点K，并将其加入到数组S中；同时，从数组U中移除顶点K。接着，更新数组U中的各顶点到起点D的距离。
  5. 重复第4步操作，直到遍历完所有顶点。
    import01.png

我的思考

图中我用绿色标记已经存入S[]中的节点，黄色标记已经计算过某条路径的节点（不一定是最小值）即U[]中非无穷大的节点, “*”代表

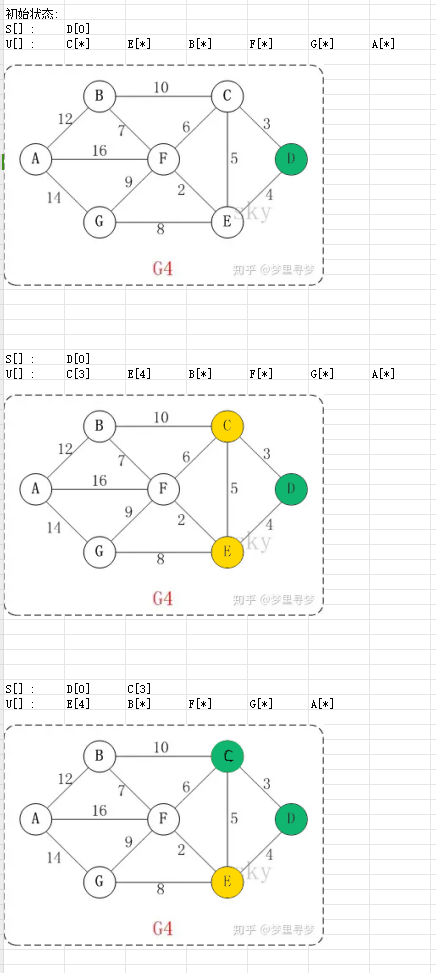
step1.png
至此,我们凭什么认为C->D已经找到了最小路径呢？

证明：
C->D由(N_d + 1)条路径组成
对于C->E->D的路径
总路径长度应小于 3
在其他C->D路径中 若与D相连的路径没有小于 3 的 此处得证
在其他C->D路径中 若与D相连的路径有小于 3 的
与第一步 选出最短节点操作相悖 该情况不存在 此处得证

 

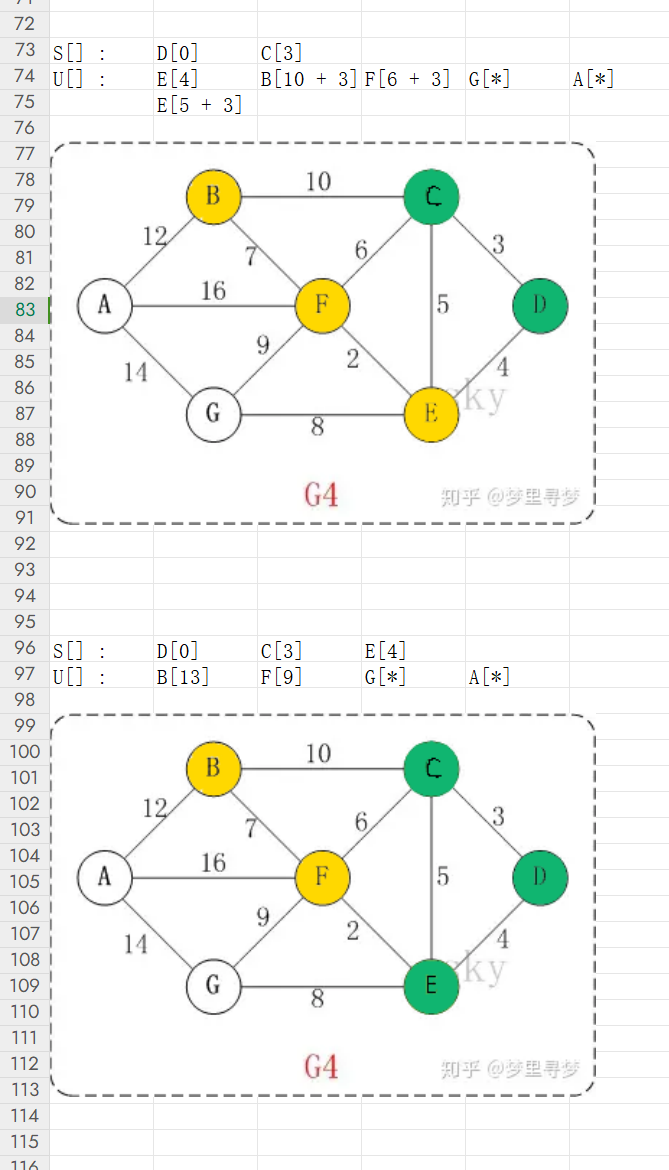
step2.png
同样的问题,我们凭什么认为E->D已经找到了最小路径呢？

证明：
对于 E->C->D 和 E->D 已完成对比 大小关系已确定
E->F->C 一定大于等于 E->C
同理 E->G->F->C 一定大于等于 E->F->C 大于等于 E->C
因此E->为最小路径

 

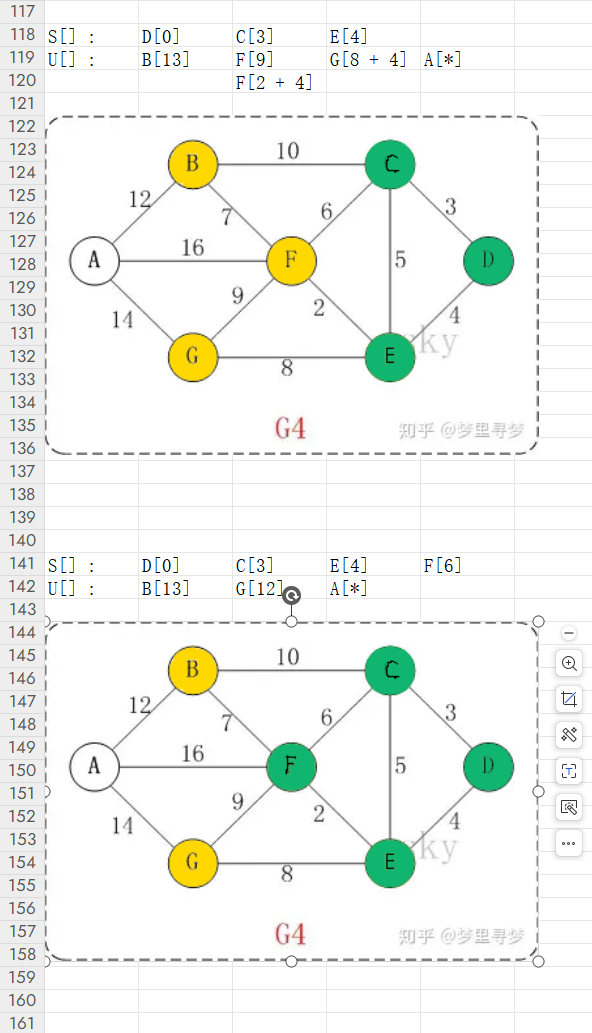
step3.png
还是那个问题,我们凭什么认为F->E->D已经找到了最小路径呢？

证明:
F->C->E->D与F->E->C->D均大于等于F->C->D和F->E->D
对于F->C->D和F->E->D 已完成比较

 

后续的步骤: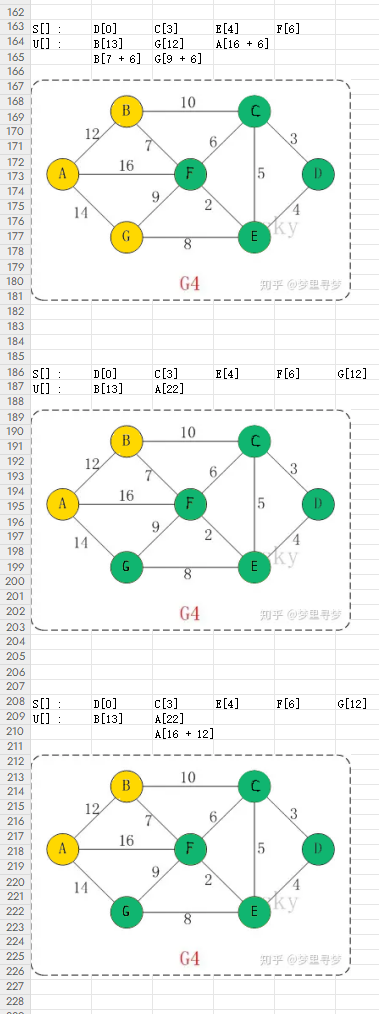
step4.png
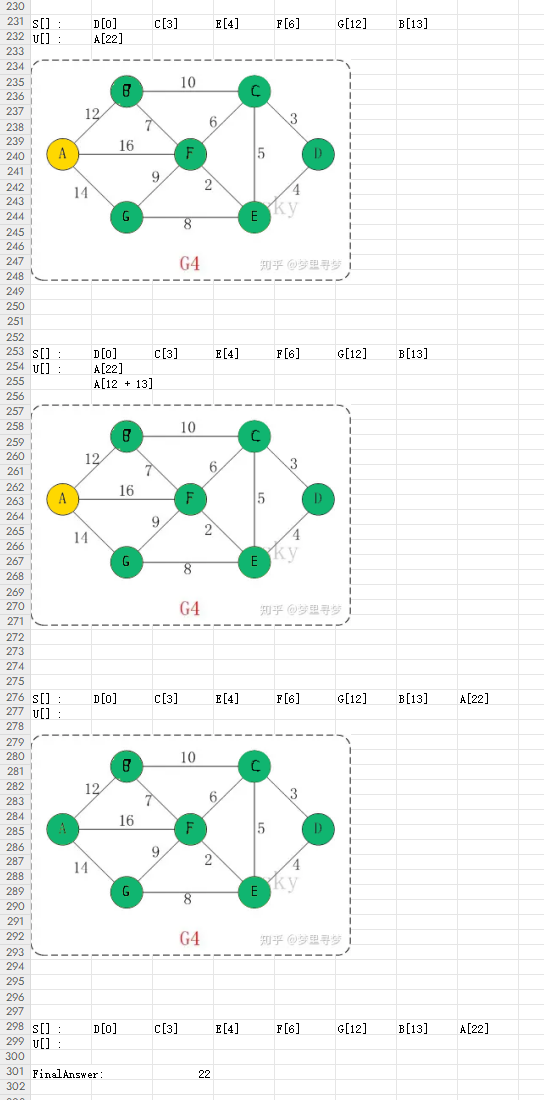
step5.png

规律总结

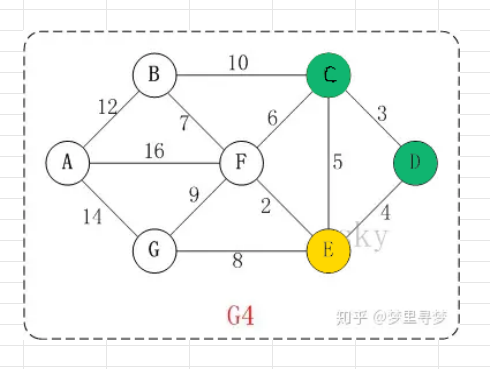
step6.png

先回到这一步
对于E 非全绿路径路径数一定多于或等于全绿路径
因此非全绿路径的路径长一定大于或等于全绿路径的路径长
而对于全绿路径，每个路径都会在之前的绿节点确认时进行了充分的对比

总结

Dijkstra算法始终在求解一个问题：

|—-|
|接下来，哪一个顶点会是下一个被找出最短路径的节点？?|

 
 

代码实现

参考实现方法:路径规划求最短路径——Dijkstra算法一步一步讲清楚（附代码/可执行）_dijkstra算法步骤-CSDN博客

我使用了一个二维数组weightTable来存储顶点之间的关系
另一个二维数组connectionTable来记录各个顶点是否相互连接
一个结构体数组DistanceTable来代替传统的S[]和U[]两个数组，用来记录某个顶点是否已经是确定状态（已经达到最小值，也就是上文途中的绿色节点）和当前最小值
十六进制数0x7fffffff是int类型的最大值，用于表示无穷大

代码:

Dijkstra.hpp 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
#pragma once
#include <iostream>
using std::cout;
using std::cin;
using std::endl;

class Dijkstra {
protected:
	bool IfLegal(int nodeNumber) {
		if (nodeNumber >= 0 && nodeNumber <= nodeAccount - 1) {
			return true;
		}
		return false;
	}

	int FindAdjacentNearestNode(int nodeNumber) {
		int nearestNodeWeight = 0x7fffffff;
		int nearestNode = -1;
		int totalWeight;
		int i;
		for (i = 0; i < this->nodeAccount; i++) {
			//cout << "i=" << i << ", nodeNumber=" << nodeNumber << endl;
			//cin.get();
			if (i != nodeNumber && DistanceTable[i]->ifConfirm != true) {
				totalWeight = DistanceTable[nodeNumber]->shortestDistance + weightTable[nodeNumber][i];
				cout << endl << "i=" << i << ", nodeNumber=" << nodeNumber << endl;
				cout << "weightTable[nodeNumber][i]=" << weightTable[nodeNumber][i] << endl;
				cin.get();
				if (connectionTable[nodeNumber][i] && totalWeight < DistanceTable[i]->shortestDistance) {
					DistanceTable[i]->shortestDistance = totalWeight;
				}
			}
		}
		//cout << "nearestNode=" << nearestNode << endl;
		//cin.get();
		for (int i = 0; i < nodeAccount; i++) {
			if (DistanceTable[i]->ifConfirm == false && DistanceTable[i]->shortestDistance < nearestNodeWeight) {
				nearestNodeWeight = DistanceTable[i]->shortestDistance;
				nearestNode = i;
			}
		}
		if (nearestNode != -1) {
			DistanceTable[nearestNode]->ifConfirm = true;
		}
		return nearestNode;
	}
public:
	Dijkstra(int nodeAccount) {
		this->nodeAccount = nodeAccount;
		weightTable = new int* [this->nodeAccount];
		for (int i = 0; i < this->nodeAccount; i++) {
			weightTable[i] = new int[this->nodeAccount];
			for (int j = 0; j < this->nodeAccount; j++) {
				weightTable[i][j] = 0x7fffffff;
			}
		}
		connectionTable = new bool* [this->nodeAccount];
		for (int i = 0; i < this->nodeAccount; i++) {
			connectionTable[i] = new bool[this->nodeAccount];
			for (int j = 0; j < this->nodeAccount; j++) {
				connectionTable[i][j] = false;
			}
		}
		DistanceTable = new NodeAttribute * [this->nodeAccount];
		for (int i = 0; i < this->nodeAccount; i++) {
			DistanceTable[i] = new NodeAttribute;
			DistanceTable[i]->ifConfirm = false;
			DistanceTable[i]->shortestDistance = 0x7fffffff;
		}
	}

	bool BuildLink(int beginNode, int endNode, int weight) {
		if (IfLegal(beginNode) && IfLegal(endNode)) {
			weightTable[beginNode][endNode] = weight;
			connectionTable[beginNode][endNode] = true;
			weightTable[endNode][beginNode] = weight;
			connectionTable[endNode][beginNode] = true;
			return true;
		}
		return false;
	}

	bool GetIndex(int rootNode, int* receiveArray, int arraySize) {
		if (arraySize != this->nodeAccount) {
			return false;
		}
		DistanceTable[rootNode]->shortestDistance = 0;
		DistanceTable[rootNode]->ifConfirm = true;
		int nextNode = FindAdjacentNearestNode(rootNode);
		for (int i = 0; i < nodeAccount; i++) {
			if (nextNode == -1) {
				break;
			}
			nextNode = FindAdjacentNearestNode(nextNode);
		}
		for (int i = 0; i < nodeAccount; i++) {
			receiveArray[i] = DistanceTable[i]->shortestDistance;
		}
		return true;
	}

	~Dijkstra() {
		for (int i = 0; i < this->nodeAccount; i++) {
			delete[] weightTable[i];
			delete[] connectionTable[i];
			delete DistanceTable[i];
		}
		delete[] weightTable;
		delete[] connectionTable;
		delete[] DistanceTable;
	}
private:
	int nodeAccount;
	int** weightTable;
	bool** connectionTable;
	struct NodeAttribute {
		bool ifConfirm;
		int shortestDistance;
	};
	NodeAttribute** DistanceTable;
};

 

main.cpp 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
#include"Dijkstra.hpp"
using namespace std;

int main() {
	Dijkstra DijkstraMap(7);
	DijkstraMap.BuildLink(0, 1, 12);
	DijkstraMap.BuildLink(0, 5, 16);
	DijkstraMap.BuildLink(0, 6, 14);
	DijkstraMap.BuildLink(1, 2, 10);
	DijkstraMap.BuildLink(1, 5, 7);
	DijkstraMap.BuildLink(6, 5, 9);
	DijkstraMap.BuildLink(6, 4, 8);
	DijkstraMap.BuildLink(5, 2, 6);
	DijkstraMap.BuildLink(5, 4, 2);
	DijkstraMap.BuildLink(2, 4, 5);
	DijkstraMap.BuildLink(2, 3, 3);
	DijkstraMap.BuildLink(4, 3, 4);
	int result[7];
	DijkstraMap.GetIndex(3, result, 7);
	for (int i = 0; i < 7; i++) {
		cout << result[i] << endl;
	}
}

以上代码托管于：我的github仓库

Author：M1MisakaMikoto
Link：http://m1misakamikoto.github.io/2023/11/01/Dijkstra%E7%AE%97%E6%B3%95%E6%B1%82%E6%9C%80%E7%9F%AD%E8%B7%AF%E5%BE%84/
版权声明：本文采用 CC BY-NC-SA 3.0 CN 协议进行许可
×